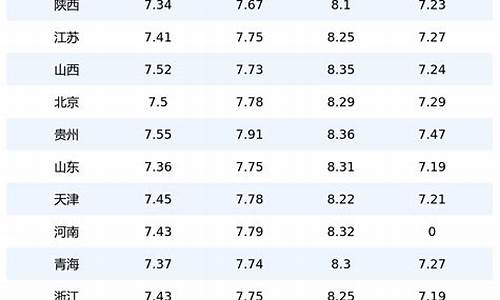
有关油价选择题及答案_油价相关

1.经济学相关题目，答案是B，求 画出图像并分析答案，谢谢

2.某石油进口国这个月的石油进口量比上个月减少5%，由于国际油价上涨，这个月进口石

3.几道初三的数学题，求解答，希望过程详细点！

4.英语选择题单选题（托业），求助解析分析答案

5.初中数学联赛试题提供2006—2009

6.按今日92油价6.5元每升来算，百公里12个油，相当于每公里要花费多少钱，求公式解答

根据你的提问，你不必报油价就可以。200元÷230公里≈0.87元/公里。如果你想根据这些数据计算你车的油耗，那么200元÷6.46元/升再÷230公里再乘以100≈13.5升/百公里。根据你提供的数据看，你的车够费油的。

经济学相关题目，答案是B，求 画出图像并分析答案，谢谢

某石油进口国这个月的石油进口量比上个月减少5%，由于国际油价上涨，这个月进口石

新的均衡是的均衡产量和均衡价格解释如图：

油价上涨了，那么需求就会降低；成本降低了，那么供给增加，供给增加而需求降低，那么均衡价格就会下降。

但是均衡产量不确定，简单点说就是：如油价上涨一点点，而汽车成本降低很多带来价格下降很多，反而销量会变大。反之油价涨的多，而成本减的少带来的价格下降少，那么均衡销量就会下降。

几道初三的数学题，求解答，希望过程详细点！

你的问题还没说完。所以，我也不知道是哪个，不过我恰巧做这个（是黄冈100分吧），是不是这道题：某石油进口国这个月的石油进口量比上个月减少了5%，由于国际油价上涨，这个月进口石油的反而而比上个月增加了14%。求这个月石油价格相对上个月的增长率。解答方法：

解：设这个月的石油价格相对上个月的增长率为x。根据题意得

（1＋x）（1－5%）=1＋14%

解得x=1/5=20%

答案就这么写的哦！

其实你把这题打到网上，就有，不用等着了

英语选择题单选题（托业），求助解析分析答案

1、设上个月进口量A，油价B，则这个月进口量（1-5%）A，

这个月的油价=AB(1+14%)/[(1-5%)A]=6B/5

这个月的油价相对于上个月的增长率=(6B/5-B)/B=1/5=20%

2、D

3、把5和10米带进去自己算

初中数学联赛试题提供2006—2009

1. C

此处应该是 such as， such 为省略。

2. D

the only means of mobility ailable 意思是唯一可用的移动方式。technique技巧 roach 方法 instrument 工具 means 方法、手段 。根据文意，means 最为合适。

3. B

个人认为，后面为时间状语从句，用一般现在始就可。

按今日92油价6.5元每升来算，百公里12个油，相当于每公里要花费多少钱，求公式解答

2008年全国初中数学联赛

2008年4月13日上午8：30—9：30

一、选择题：（本题满分42分，每小题7分）

1、设a 2 + 1 = 3 a，b 2 + 1 = 3 b，且a ≠ b，则代数式 + 的值为（ ）

（A）5 （B）7 （C）9 （D）11

2、如图，设AD，BE，CF为△ABC的三条高，若AB = 6，BC = 5，EF = 3，则线段BE的长为（ ）

（A） （B）4 （C） （D）

3、从分别写有数字1，2，3，4，5的5张卡片中任意取出两张，把第一张卡片上的数字作为十位数字，第二张卡片上的数字作为个位数字，组成一个两位数，则所组成的数是3的倍数的概率是（ ）

（A） （B） （C） （D）

4、在△ABC中，∠ABC = 12°，∠ACB = 132°，BM和CN分别是这两个角的外角平分线，且点M，N分别在直线AC和直线AB上，则（ ）

（A）BM > CN （B）BM = CN （C）BM < CN （D）BM和CN的大小关系不确定

5、现有价格相同的5种不同商品，从今天开始每天分别降价10％或20％，若干天后，这5种商品的价格互不相同，设最高价格和最低价格的比值为r，则r的最小值为（ ）

（A）( ) 3 （B）( ) 4 （C）( ) 5 （D）

6、已知实数x，y满足( x – ) ( y – ) = 2008，

则3 x 2 – 2 y 2 + 3 x – 3 y – 2007的值为（ ）

（A）– 2008 （B）2008 （C）– 1 （D）1

二、填空题：（本题满分28分，每小题7分）

1、设a = ，则 = 。

2、如图，正方形ABCD的边长为1，M，N为BD所在直线上的两点，且AM = ，∠MAN = 135°，则四边形AMCN的面积为 。

3、已知二次函数y = x 2 + a x + b的图象与x轴的两个交点的横坐标分别为m，n，且| m | + | n | ≤ 1。设满足上述要求的b的最大值和最小值分别为p，q，则| p | + | q | = 。

4、依次将正整数1，2，3，…的平方数排成一串：149162536496481100121144…，排在第1个位置的数字是1，排在第5个位置的数字是6，排在第10个位置的数字是4，排在第2008个位置的数字是 。

答案： B、D、C、B、B、D；– 2、 、 、1。

解答：一、1、由题设条件可知a 2 – 3 a + 1 = 0，b 2 – 3 b + 1 = 0，且a ≠ b，

所以a，b是一元二次方程x 2 – 3 x + 1 = 0的两根，故a + b = 3，a b = 1，

因此 + = = = = 7；

2、因为AD，BE，CF为△ABC的三条高，易知B，C，E，F四点共圆，

于是△AEF∽△ABC，故 = = ，即cos∠BAC = ，所以sin∠BAC = 。

在Rt△ABE中，BE = AB sin∠BAC = 6 × = ；

3、能够组成的两位数有12，13，14，15，21，23，24，25，31，32，34，35，41，42，43，45，51，52，53，54，共20个，其中是3的倍数的数为12，15，21，24，42，45，51，54，共8个，所以所组成的数是3的倍数的概率是 = ；

4、∵∠ABC = 12°，BM为∠ABC的外角平分线，∴∠MBC = ( 180° – 12° ) = 84°，

又∠BCM = 180° –∠ACB = 180° – 132° = 48°，∴∠BCM = 180° – 84° – 48° = 48°，∴BM = BC，又∠ACN = ( 180° –∠ACB ) = ( 180° – 132° ) = 24°，∴∠BNC = 180° –∠ABC –∠BCN = 180° – 12° – (∠ACB +∠CAN ) = 12° =∠ABC，∴CN = CB，因此，BM = BC = CN；

5、容易知道，4天之后就可以出现5种商品的价格互不相同的情况。

设5种商品降价前的价格为a，过了n天，n天后每种商品的价格一定可以

表示为a ? ( 1 – 10% ) k ? ( 1 – 20% ) n – k = a ? ( ) k ? ( ) n – k，其中k为自然数，且0 ≤ k ≤ n，要使r的值最小，五种商品的价格应该分别为：a ? ( ) i ? ( ) n – i，a ? ( ) i + 1 ? ( ) n – i – 1，a ? ( ) i + 2 ? ( ) n – i – 2，a ? ( ) i + 3 ? ( ) n – i – 3，a ? ( ) i + 4 ? ( ) n – i – 4，

其中i为不超过n的自然数，所以r的最小值为 = ( ) 4；

6、∵( x – ) ( y – ) = 2008，∴x – = =

y + ，y – = = x + ，

由以上两式可得x = y， 所以( x – ) 2 = 2008，解得x 2 = 2008，

所以3 x 2 – 2 y 2 + 3 x – 3 y – 2007 = 3 x 2 – 2 x 2 + 3 x – 3 x – 2007 = x 2 – 2007 = 1；

二、1、∵a 2 = ( ) 2 = = 1 – a，∴a 2 + a = 1，∴原式=

= = = – = – ( 1 + a + a 2 ) = – ( 1 + 1 ) = – 2；

2、设BD中点为O，连AO，则AO⊥BD，AO = OB = ，MO = = ，

∴MB = MO – OB = 。又∠ABM =∠NDA = 135°，

∠NAD =∠MAN –∠DAB –∠MAB = 135° – 90° –∠MAB = 45°–∠MAB =∠AMB，

所以△ADN∽△MBA，故 = ，从而DN = ? BA = × 1 = ，根据对称性可知，

四边形AMCN的面积S = 2 S△MAN = 2 × × MN × AO = 2 × × ( + + ) × = ；

3、根据题意，m，n是一元二次方程x 2 + a x + b = 0的两根，所以m + n = – a，m n = b。

∵| m | + | n | ≤ 1，∴| m + n | ≤ | m | + | n | ≤ 1，| m – n | ≤ | m | + | n | ≤ 1。

∵方程x 2 + a x + b = 0的判别式△= a 2 – 4 b ≥ 0，∴b ≤ = ≤ 。

4 b = 4 m n = ( m + n ) 2 – ( m – n ) 2 ≥ ( m + n ) 2 – 1 ≥ – 1，故b ≥ – ，等号当m = – n = 时取得；4 b = 4 m n = ( m + n ) 2 – ( m – n ) 2 ≤ 1 – ( m – n ) 2 ≤ 1，故b ≤ ，等号当m = n = 时取得。所以p = ，q = – ，于是| p | + | q | = ；

4、1 2到3 2，结果都只各占1个数位，共占1 × 3 = 3个数位；4 2到9 2，结果都只各占2个数位，共占2 × 6 = 12个数位；10 2到31 2，结果都只各占3个数位，共占3 × 22 = 66个数位；32 2到99 2，结果都只各占4个数位，共占4 × 68 = 272个数位；100 2到316 2，结果都只各占5个数位，共占5 × 217 = 1085个数位；此时还差2008 – ( 3 + 12 + 66 + 272 + 1085 ) = 570个数位。317 2到411 2，结果都只各占6个数位，共占6 × 95 = 570个数位。所以，排在第2008个位置的数字恰好应该是411 2的个位数字，即为1；

2008年全国初中数学联赛

2008年4月13日上午10：00—11：30

第二试 （A）

一、（本题满分20分）已知a 2 + b 2 = 1，对于满足条件0 ≤ x ≤ 1的一切实数x，不等式a ( 1 – x ) ( 1 – x – a x ) – b x ( b – x – b x ) ≥ 0 （1）恒成立，当乘积a b取最小值时，求a，b的值。

解：整理不等式（1）并将a 2 + b 2 = 1代入，得( 1 + a + b ) x 2 – ( 2 a + 1 ) x + a ≥ 0 （2），

在（2）中，令x = 0，得a ≥ 0；令x = 1，得b ≥ 0。易知1 + a + b > 0，0 < < 1，

故二次函数y = ( 1 + a + b ) x 2 – ( 2 a + 1 ) x + a的图象（抛物线）的开口向上，且顶点的横坐标在0和1之间。由题设知，不等式（2）对于满足条件0 ≤ x ≤ 1的一切实数x恒成立，所以它的判别式△= ( 2 a + 1 ) 2 – 4 a ( 1 + a + b ) ≤ 0，即a b ≥ 。由方程组 （3）

消去b，得16 a 4 – 16 a 2 + 1 = 0，所以a 2 = 或a 2 = 。又因为a ≥ 0，

所以a 1 = 或a 2 = ，于是b 1 = 或b 2 = 。所以a b的最小值为 ，此时a，b的值分别为a = ，b = 和a = ，b = 。

二、（本题满分25分）如图，圆O与圆D相交于A，B两点，BC为圆D的切线，点C在圆O上，且AB = BC。

（1）证明：点O在圆D的圆周上；

（2）设△ABC的面积为S，求圆D的的半径r的最小值。

解：（1）连OA，OB，OC，AC，因为O为圆心，AB = BC，所以△OBA∽△OBC，从而∠OBA =∠OBC，因为OD⊥AB，DB⊥BC，所以∠DOB = 90° –∠OBA = 90° –∠OBC =∠DBO，所以DB = DO，因此点O在圆D的圆周上；

（2）设圆O的半径为a，BO的延长线交AC于点E，易知BE⊥AC。设AC = 2 y（0 < y ≤ a），OE = x，AB = l，则a 2 = x 2 + y 2，S = y ( a + x )，

l 2 = y 2 + ( a + x ) 2 = y 2 + a 2 + 2 a x + x 2 = 2 a 2 + 2 a x = 2 a ( a + x ) = 。

因为∠ABC = 2∠OBA = 2∠OAB =∠BDO，AB = BC，DB = DO，所以△BDO∽△ABC，

所以 = ，即 = ，故r = ，所以r 2 = = ? = ? ( ) 3 ≥ ，即r ≥ ，其中等号当a = y时成立，这时AC是圆O的直径.所以圆D的的半径r的最小值为 。

三、（本题满分25分）设a为质数，b为正整数，且9 ( 2 a + b ) 2 = 509 ( 4 a + 511 b ) （1）

求a，b的值。

解：（1）式即( ) 2 = ，设m = ，n = ，则n = m 2，

b = = （2），故3 n – 511 m + 6 a = 0，所以3 m 2 – 511 m + 6 a = 0 （3），由（1）式可知，( 2 a + b ) 2能被质数509整除，于是2 a + b能被509整除，故m为整数，

即关于m的一元二次方程（3）有整数根，所以它的判别式△= 511 2 – 72 a为完全平方数。

不妨设△= 511 2 – 72 a = t 2（ 为自然数），则72 a = 511 2 – t 2 = ( 511 + t ) ( 511 – t )，

由于511 + t和511 – t的奇偶性相同，且511 + t ≥ 511，所以只可能有以下几种情况：

① ，② ，③ ，④ ，两式相加分别得

36 a + 2 = 1022，18 a + 4 = 1022，12 a + 6 = 1022，6 a + 12 = 1022，均没有整数解；

⑤ ，⑥ ，两式相加分别得4 a + 18 = 1022，解得a = 251；

2 a + 36 = 1022，解得a = 493，而493 = 17 × 29不是质数，故舍去。综合可知a = 251。

此时方程（3）的解为m = 3或m = （舍去）。

把a = 251，m = 3代入（2）式，得b = = 7。

第二试 （B）

一、（本题满分20分）已知a 2 + b 2 = 1，对于满足条件x + y = 1，x y ≥ 0的一切实数对( x，y )，不等式a y 2 – x y + b x 2 ≥ 0 （1）恒成立，当乘积a b取最小值时，求a，b的值。

解：由x + y = 1，x y ≥ 0可知0 ≤ x ≤ 1，0 ≤ y ≤ 1。在（1）式中，令x = 0，y = 1，得a ≥ 0；令x = 1，y = 0，得b ≥ 0。将y = 1 – x代入（1）式，得a ( 1 – x ) 2 – x ( 1 – x ) + b x 2 ≥ 0，

即( 1 + a + b ) x 2 – ( 2 a + 1 ) x + a ≥ 0 （2），易知1 + a + b > 0，0 < < 1，

故二次函数y = ( 1 + a + b ) x 2 – ( 2 a + 1 ) x + a的图象（抛物线）的开口向上，且顶点的横坐标在0和1之间。由题设知，不等式（2）对于满足条件0 ≤ x ≤ 1的一切实数x恒成立，

所以它的判别式△= ( 2 a + 1 ) 2 – 4 a ( 1 + a + b ) ≤ 0，即a b ≥ 。由方程组 （3）消去b，得16 a 4 – 16 a 2 + 1 = 0，所以a 2 = 或a 2 = 。又因为a ≥ 0，

所以a 1 = 或a 2 = ，于是b 1 = 或b 2 = 。所以a b的最小值为 ，此时a，b的值分别为a = ，b = 和a = ，b = 。

二、（本题满分25分）题目和解答与（A）卷第二题相同。

三、（本题满分25分）题目和解答与（A）卷第三题相同。

第二试 （C）

一、（本题满分25分）题目和解答与（B）卷第一题相同。

二、（本题满分25分）题目和解答与（A）卷第二题相同。

三、（本题满分25分）设a为质数，b，c为正整数，且满足 ，求a ( b + c )的值。

解：（1）式即( ) 2 = ，设m = ，n = ，则2 b – c = = （3），故3 n – 511 m + 6 a = 0，又n = m 2，

所以3 m 2 – 511 m + 6 a = 0 （4），由（1）式可知，( 2 a + 2 b – c ) 2能被509整除，

而509是质数，于是2 a + 2 b – c能被509整除，故m为整数，

即关于m的一元二次方程（4）有整数根，所以它的判别式△= 511 2 – 72 a为完全平方数。

不妨设△= 511 2 – 72 a = t 2（ 为自然数），则72 a = 511 2 – t 2 = ( 511 + t ) ( 511 – t )，

由于511 + t和511 – t的奇偶性相同，且511 + t ≥ 511，所以只可能有以下几种情况：

① ，② ，③ ，④ ，两式相加分别得

36 a + 2 = 1022，18 a + 4 = 1022，12 a + 6 = 1022，6 a + 12 = 1022，均没有整数解；

⑤ ，⑥ ，两式相加分别得4 a + 18 = 1022，解得a = 251；

2 a + 36 = 1022，解得a = 493，而493 = 17 × 29不是质数，故舍去。综合可知a = 251。

此时方程（3）的解为m = 3或m = （舍去）。

把a = 251，m = 3代入（3）式，得2 b – c = = 7，即c = 2 b – 7，代入（2）式得b – ( 2 b – 7 ) = 2，所以b = 5，c = 3，因此a ( b + c ) = 251 × ( 5 + 3 ) = 2008。

相当于每公里要花费0.78元。

根据题意，油价为6.5元/升，一百公里耗油12L，

那么一百公里所需花费=12*6.5=78（元）

那么运用除法，列式可得：

每公里油钱=78/100=0.78（元）

扩展资料：

降低油耗的办法：

一、夏日检查空调系统检查必不可少

空调故障可能也是耗油很重要的原因，如果空调制冷效果不好，不少人会加大风速和降低温度，以达到凉爽的效果。

鉴于空调将直接影响夏天汽车的油耗，车主一定要及时对空调进行保养和检查。值得一提的是，除了空调故障外，空调的散热网（冷凝器）布满灰尘等也会直接影响散热效果，车主应及时对冷凝器进行清洁，确保空调以良好的状态工作。

二、频繁急刹是导致油耗居高的主因

频繁的急刹，是导致汽车油耗居高不下的主因。而来自具备储存动能的油电混合动力车型数据显示，其油耗比同级别的车型低40%左右，从这个侧面的数据也反映，市区综合耗油的偏高，与频繁的急刹，关系明显。

在确保车辆安全行驶的同时，充分利用车辆的惯性。以前面300米处有一红灯位为例，车辆速度只需提到40公里/小时，就可通过惯性滑行到路口。但不少车主在行驶时，继续加速，在接近红绿灯路口时时速已达到60公里/小时，就只好狂踩刹车，加速时的油耗就白白浪费了。

提醒：驾驶时只有在遭遇紧急情况才会大力踩刹车，在接近路口和停车都应是保持温柔踩刹车。如果你的右脚长期处于高强度的使用刹车和油门状态，那充分说明你的驾驶习惯需要及时地纠正。

三、依靠惯性行驶是节油的关键

“惯性行车”省油众所周知，但在实际的调查发现，真正能用好惯性行车的车主，并不多见。记者就“踩刹车的时间和踩油门的时间”针对经常在禅城城区驾驶的近二十名车主的随机访发现，超过半数的车主表示，踩刹车至少占市区行驶时间的1/3，车多、红绿灯多是主因。

四、小排量车空调不宜开启过猛

在太阳底下暴晒的车辆，上车后不宜立即开启空调。合理的做法是开启车窗（也可把车门打开），在不开启空调的前提下把风机调置较高档位，驱赶走车内的热气，等车辆适度降温后，再开启空调。

除了恰当开启空调外，在行驶时，风机的风速应尽量调低。空调温度设置不宜太低，一般在25℃左右较为适宜。对于非自动恒温的手动调节的空调，建议关闭无人乘坐的副驾驶风口，让冷气集中在驾驶室上，这样能够有效地节能油耗。

百度百科—油耗